深度学习Pytorch——神经网络

一、简介

神经网络可以通过torch.nn包构建，上一节已经对自动梯度有些了解，神经网络是基于自动梯度来定义一些模型。一个nn.Module包括层和一个方法，它会返回输出。例如：数字图片识别的网络：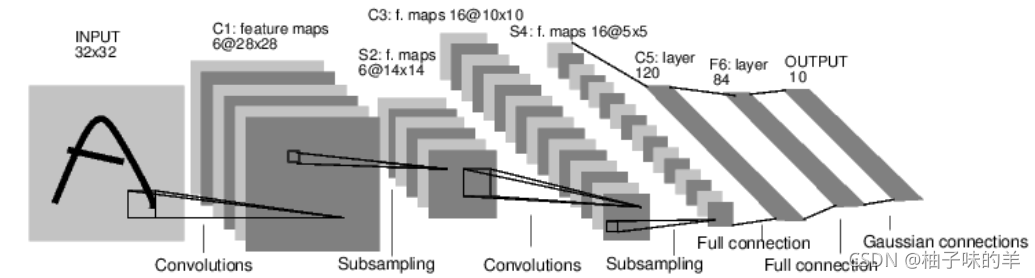

上图是一个简单的前回馈神经网络，它接收输入，让输入一个接着一个通过一些层，最后给出输出。

二、神经网络训练过程

一个典型的神经网络训练过程包括一下几点：

1. 定义一个包含可以训练参数的神经网络
2. 迭代整个输入
3. 通过神经网络处理输入
4. 计算损失
5. 反向传播梯度到神经网络的参数
6. 更新网络的参数（典型的一个简单的更新方法是：weight=weight-learning_rate*gradient）

三、实例演示

1、定义一个神经网络

# -*- coding: utf-8 -*- """ Created on Sun Oct 24 15:56:23 2021 @author: Lenovo """ # 神经网络 # import torch import torch.nn as nn import torch.nn.functional as F  class Net(nn.Module):          def __init__(self):         super(Net,self).__init__()         # 1个输入，6个输出，5*5的卷积         # 内核         self.conv1=nn.Conv2d(1,6,5)         self.conv2=nn.Conv2d(6,16,5)         # 映射函数：线性——y=Wx+b         self.fc1=nn.Linear(16*5*5,120)#输入特征值：16*5*5，输出特征值：120         self.fc2=nn.Linear(120,84)         self.fc3=nn.Linear(84,10)              def forward(self,x):         x=F.max_pool2d(F.relu(self.conv1(x)),(2,2))         # 如果其尺寸是一个square只能指定一个数字         x=F.max_pool2d(F.relu(self.conv2(x)),2)         x=x.view(-1,self.num_flat_features(x))         x=F.relu(self.fc1(x))         x=F.relu(self.fc2(x))         x=self.fc3(x)         return x          def num_flat_features(self,x):         size=x.size()[1:]         num_features=1         for s in size:             num_features *= s         return num_features                         net=Net() print(net) 

运行结果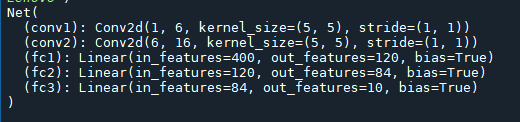

以上定义了一个前馈函数，然后反向传播函数被自动通过autograd定义，可以使用任何张量操作在前馈函数上。

2、通过调用net.parameters()返回模型可训练的参数

# 查看模型可训练的参数 params=list(net.parameters()) print(len(params)) print(params[0].size())# conv1 的权重weight 

运行结果

3、迭代整个输入

尝试随机生成一个3232的输入。注：期望的输入维度是3232，为了在MNIST数据集上使用这个网络，我们需要把数据集中的图片维度修改为32*32

input=torch.randn(1, 1, 32,32) print(input) out=net(input) print(out) 

运行结果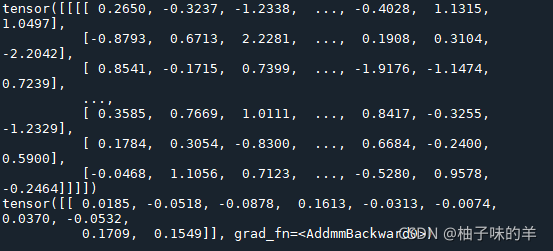

4、调用反向传播

将所有参数梯度缓存器置零，用随机的梯度来反向传播

# 调用反向传播 net.zero_grad() out.backward(torch.randn(1, 10)) 

运行结果

5、计算损失值

#计算损失值——损失函数：一个损失函数需要一对输入：模型输出和目标，然后计算一个值来评估输出距离目标多远。有一些不同的损失函数在nn包中，一个简单的损失函数就是nn.MSELoss，他计算了均方误差

如果跟随损失到反向传播路径，可以使用他的.grad_fn属性，将会看到一个计算图 

# 在调用loss.backward()时候，整个图都会微分，而且所有的图中的requires_grad=True的张量将会让他们的grad张量累计梯度 #跟随以下步骤反向传播 print(loss.grad_fn)#MSELoss print(loss.grad_fn.next_functions[0][0])#Linear print(loss.grad_fn.next_functions[0][0].next_functions[0][0])#relu 

运行结果

6、反向传播梯度

为了实现反向传播loss，我们所有需要做的事情仅仅是使用loss.backward()。需要先清空现存的梯度，不然梯度将会和现存的梯度累计在一起。

# 调用loss.backward()然后看一下con1的偏置项在反向传播之前和之后的变化 net.zero_grad() print('conv1.bias.grad before backward') print(net.conv1.bias.grad) loss.backward()#反向传播 print('conv1.bias.grad after backward') print(net.conv1.bias.grad) 

运行结果

7、更新神经网络参数

# ============================================================================= # # 最简单的更新规则就是随机梯度下降:weight=weight-learning_rate*gradient # learning_rate=0.01 # for f in net.parameters(): #     f.data.sub_(f.grad.data*learning_rate)#f.data=f.data-learning_rate*gradient #  ============================================================================= 

如果使用的是神经网络，想要使用不同的更新规则，类似于SGD,Nesterov-SGD,Adam,RMSProp等。为了让这可行，Pytorch建立一个称为torch.optim的package实现所有的方法，使用起来更加方便

# ============================================================================= # import torch.optim as optim # optimizer=optim.SGD(net.parameters(), lr=0.01) # # 在迭代训练过程中 # optimizer.zero_grad()#将现存梯度置零 # output=net(input) # loss=criterion(output,target) # loss.backward()#反向传递 # optimizer.step()#更新网络参数 # ============================================================================= 

记得神经网络训练过程（part 二），其中最重要的还是梯度。记得反向传播~
今日告一段落，明儿见~